对于材料的疲劳损伤与寿命预测,经典的Basquin公式(1910年)与Coffin-Manson公式(1954年)分别选择应力幅与塑性应变幅为参量进行评价。然而,鉴于疲劳实验中应力幅和应变幅的差异,同一组数据经由不同疲劳模型分析后会产生迥异的规律(图1)。因此,疲劳损伤参量的合理选择成为正确认识疲劳损伤本质与规律的先决条件。针对这一问题,沈阳材料科学国家(联合)实验室材料疲劳与断裂研究部张哲峰研究员课题组经过长期系统的研究,提出了以能量作为主要损伤参量的滞回能模型。
1. 模型建立:以循环变形过程中的滞回能为材料疲劳损伤输入的总塑性功,定义有效转化为疲劳损伤的参量为D=1/Nf=(Wa/W0)β,其中,W0 代表材料的本征疲劳韧性,β 为疲劳损伤转化指数,代表外界输入能量转化成损伤材料的能力,二者均具有明确的物理意义:1)W0 与静力韧性U 呈正相关关系,代表材料的疲劳损伤容限;2) β 与微观变形机制相关,代表疲劳损伤累积速率。因此,该模型能够更加客观地评价材料的疲劳性能和预测其疲劳寿命。同时,考虑恒应力幅与恒应变幅疲劳的特殊条件,可证明经典的Basquin公式与Coffin-Manson公式均为该能量模型的简化形式,这进一步反映了该模型的合理性与普适性。
2. 模型应用:在Cu-Al合金与Fe-Mn-C钢中,发现疲劳韧性W0 随其强韧性的同步提高均呈现出线性增加的趋势,而疲劳损伤转化指数β 却随之表现出截然相反的趋势(图2a,b)。进一步分析发现,β 的不同趋势由微观变形行为的差异所导致(图2c,d)。模型参数与塑性变形机制的契合从微观上证实了该能量模型的合理性。由此可知,疲劳损伤本质上可看作能量累积的过程,提高疲劳损伤容限(开源)与降低疲劳损伤累积速率(节流)是提高各种材料疲劳性能的根本手段(图3)。
上述研究工作发表在Acta Materialia 83 (2015) 341、Acta Materialia 103 (2016) 781和Scientific Reports 5 (2015) 9550上。
该项工作得到国家杰出青年科学基金与重点基金的资助。
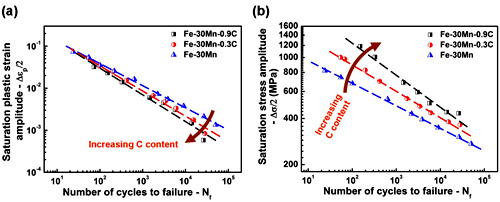
图1. Fe-Mn-C钢的疲劳寿命曲线:(a)塑性应变幅-寿命曲线(Coffin-Mansion公式);(b)应力幅-寿命曲线(Basquin公式)。采用应力与应变作为参数评价材料的疲劳寿命表现出相反的趋势
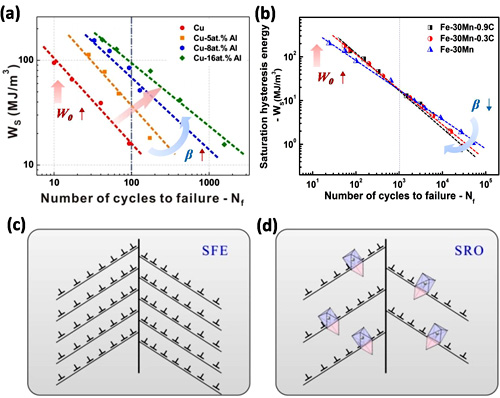
图2. 滞回能模型的应用:(a)Cu-Al合金能量-寿命曲线;(b)Fe-Mn-C钢能量-寿命曲线;层错能(SFE)和短程有序(SRO)对(c) Cu-Al合金微观变形机制与(d)Fe-Mn-C钢微观变形机制影响示意图
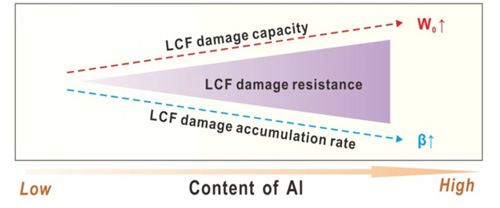
图3. 材料疲劳寿命提高的策略:提高材料的疲劳损伤容限(开源)与降低材料的疲劳损伤累积速率(节流)



